Introdução
Precisei normalizar os nomes de alguns genes humanos e inicialmente pensei que seria uma tarefa fácil, porém ao analisar as saídas, verifiquei que nem todos os nomes foram normalizados. O problema evoluiu e encontrei a solução lá na área de Teoria de Grafos.
A postagem de hoje é para resolver qualquer problema em que entidades (ex: genes) podem ser referenciadas por vários outros nomes em que tais nomes não estão agrupados de forma estruturada, mas sim espalhados por todo um banco de dados.
O problema
Suponha que você tenha essa cadeia de nomes:
A,B,C,D,E,F
O que ela diz é que A é sinônimo de B, de C, de E, etc. Também diz que B e C, B e D, etc são sinônimos. Basicamente, de forma geral, onde aparecer qualquer uma dessas letras, está se referenciando a mesma entidade. Um processo de normalização seria quando aparecer as letras {B,C,D,E,F} trocar pela a letra {A}, por exemplo.
Agora, suponha que você tenha várias dessas cadeias:
A,B,C,D,E,F K,L,O J,M,D M,O,P,E
seguindo o mesmo padrão, todos os símbolos na mesma linha representam a mesma entidade. Como podemos ver, há um problema nessa abordagem. A terceira linha contém o símbolo “D”, indicando que {J,M} também referencia a mesma entidade que {A,B,C,E,F}.
O mesmo ocorre na última linha, onde aparece o símbolo E, o que acrescenta mais três nomes novos, {M,O,P}, para representar a mesma entidade. Ainda mais, o “O” aparece na segunda linha, o que faz que todos os nomes mostrados representem a mesma entidade.
Todas as linhas poderiam ser reduzidas a:
A,B,C,D,E,F,K,L,J,M,O,P
O problema está em encontrar tal redução dado que os nomes estão espalhados no arquivo de entrada.
Vantagem de nomes únicos
Uma vantagem de normalizar nomes é que se entidades se relacionam entre si (ex: um grafo), o uso de nomes únicos aumenta o número de relações (alguns vértices se tornam o mesmo), torna o grafo mais denso e, consequentemente, menor.
É só imaginar que se um grafo era formado por:
A -> X E -> Y P -> X
então o novo grafo será formado somente por:
A -> X A -> Y
já que P -> X é duplicado e E tem o mesmo nome de A.
A solução ingênua
A solução ingênua seria pegar cada nome de uma linha e verificar se ele aparece no restante do arquivo. Se sim, junte as linhas em que ele aparece e recomece a busca usando outro nome porém sem acrescentar linhas já coadunadas anteriormente. Parece um problema complexo, porque realmente é, e a complexidade estoura se o arquivo consultado for grande, pois o tempo é da ordem de n^2.
A solução: Componentes Conexas
Se você observar bem, as linhas do arquivo problema é de fato uma formulação de um grafo. Todos os nomes na mesma linha ligam entre si, como também os vértices que são referenciados em outras linhas. Logo, a solução se passa na área de Teoria de Grafos.
Se tratarmos cada nome como um vértice de um grafo e as arestas representarem os vértices associados como sinônimos, então a solução é basicamente sair de um vértice e verificar quais outros vértices são alcançáveis a partir dele. Esse conjunto de vértices contém todos os sinônimos para uma mesma entidade. Ora, isso nada mais é que encontrar as componentes conexas de um grafo não direcionado [2].
Para quem faltou as aulas de Grafos ou não conhece muito sobre o assunto, uma componente conexa (CC) é um conjunto de vértices que estão conectados, isso é, para cada par (i, j) de vértices desse conjunto, você consegue sair de i e chegar em j.
Em relação ao nosso problema, o conjunto de vértices de uma CC representa todos os nomes associados a mesma entidade. Para normalizar, basta eleger um vértice da CC como nome geral e substituir todas ocorrências dos outros vértices por esse nome.
Encontrar todas as CC’s é realizar uma busca em largura a partir de um vértice e salvar os vértices alcançáveis, depois realizar a busca novamente iniciando de outro vértice e continuar assim até que todos os vértices sejam visitados.
Código
O código eu peguei pronto de [1] e está escrito em python. Fiz uma pequena modificação para ler de um arquivo fixo de entrada, chamado de entrada.txt.
#!/usr/bin/env python
# Finding connected components in a bidirectional graph.
# By Mario Vilas (mvilas at gmail dot com)
# http://breakingcode.wordpress.com/2013/04/08/finding-connected-components-in-a-graph
# [ cc.py ]
# Modificado ligeiramente para ler de um arquivo fixo: entrada.txt
# daemoniolabs.wordpress.com
# Sat Oct 15 20:26:52 BRT 2016
# The graph nodes.
class Data(object):
def __init__(self, name):
self.__name = name
self.__links = set()
@property
def name(self):
return self.__name
@property
def links(self):
return set(self.__links)
def add_link(self, other):
self.__links.add(other)
other.__links.add(self)
# The function to look for connected components.
def connected_components(nodes):
# List of connected components found. The order is random.
result = []
# Make a copy of the set, so we can modify it.
nodes = set(nodes)
# Iterate while we still have nodes to process.
while nodes:
# Get a random node and remove it from the global set.
n = nodes.pop()
# This set will contain the next group of nodes connected to each other.
group = {n}
# Build a queue with this node in it.
queue = [n]
# Iterate the queue.
# When it's empty, we finished visiting a group of connected nodes.
while queue:
# Consume the next item from the queue.
n = queue.pop(0)
# Fetch the neighbors.
neighbors = n.links
# Remove the neighbors we already visited.
neighbors.difference_update(group)
# Remove the remaining nodes from the global set.
nodes.difference_update(neighbors)
# Add them to the group of connected nodes.
group.update(neighbors)
# Add them to the queue, so we visit them in the next iterations.
queue.extend(neighbors)
# Add the group to the list of groups.
result.append(group)
# Return the list of groups.
return result
# The test code...
if __name__ == "__main__":
f = open("entrada.txt")
LINHAS = f.readlines()
# Dicionario: key (sinonimo) => value (objeto node correspondente)
NOMES={}
for linha in LINHAS:
linha = linha.rstrip('\n')
genes = linha.split(',')
for g in genes:
if len(g) == 0: continue
if not NOMES.has_key(g):
NOMES[g]=Data(g)
for linha in LINHAS:
linha = linha.rstrip('\n')
n = linha.split(',')
if len(n) > 1:
for i in range(len(n)):
if len(n[i]) == 0: continue
for j in range(len(n)):
if len(n[j]) == 0: continue
if i != j:
a = NOMES[n[i]]
b = NOMES[n[j]]
a.add_link(b)
nodes = NOMES.values()
# Find all the connected components.
number = 1
for components in connected_components(nodes):
names = sorted(node.name for node in components)
names = ",".join(names)
#print "Group #%i:%s" % (number, names)
print names
number += 1
# You should now see the following output:
# Group #1: a, b, c, d, e, f
# Group #2: g
# Group #3: h, i, j, k
Exemplo: Genes humanos
Vejamos um exemplo mais complexo envolvendo genes humanos. Esse é um modelo do arquivo de entrada, o entrada.txt, em que linhas são nomes/sinônimos separados por vírgula.
DPCK,EEC3,ERGIC63,ERGIC_63,GPAT,HCP5,KET,CKAP4 SHFM4,TP53CP,TP53L,P63 ELAC2,FLJ10530,HPC2,CBX4 HPC8,HSPC187,NBP16,NEC2,PC2,PCAP,ELAC2 PCSK2,PC_2,PKD2,PKD4,HPC2 GCFC2,GC_F,GCF,GUC2DL,GUCY2F,RETGC2 RETGC_2,ROSGC2,ROS_GC2,TCF9,GCF AIE75,AIE_75,DFNB18, HARMONIN,NYCO37,NYCO38,NY_CO_37,NY_CO_38,PDZ73 C2ORF3,CYGF,DNABF,GCF PDZ73,PDZD7C,PDZ_73,USH1C,AIE75 TP63,TP73L,ZER6,ZNF398 CKAP4,CLIMP63,CLIMP_63,COASY,CYCSP5,D6S2650E,TP73L PRKD2,SPC2,TRPP2,PKD2 CBX4,CSAD,CSD,DKFZP586E0820 P63,P71,P73H,P73L,PPAT,PRAT,NBP KIAA1339,NBP,OFC8,P51,P53CP,P5_1,EEC3
Genes na mesma linha são sinônimos e um gene que aparece em duas linhas distintas torna essas linhas sinônimas. Um exemplo é a primeira e a última linha que compartilham o gene “EEC3”. Essas linhas também são sinônimas da penúltima linha porque esta e a última compartilham o gene “NPB”.
Vamos rodar o código cc.py para encontrar as componentes:
$ python cc.py AIE75,AIE_75,DFNB18,HARMONIN,NYCO37,NYCO38,NY_CO_37,NY_CO_38,PDZ73,PDZD7C,PDZ_73,USH1C CKAP4,CLIMP63,CLIMP_63,COASY,CYCSP5,D6S2650E,DPCK,EEC3,ERGIC63,ERGIC_63,GPAT,HCP5,KET,KIAA1339,NBP,OFC8,P51,P53CP,P5_1,P63,P71,P73H,P73L,PPAT,PRAT,SHFM4,TP53CP,TP53L,TP63,TP73L,ZER6,ZNF398 CBX4,CSAD,CSD,DKFZP586E0820,ELAC2,FLJ10530,HPC2,HPC8,HSPC187,NBP16,NEC2,PC2,PCAP,PCSK2,PC_2,PKD2,PKD4,PRKD2,SPC2,TRPP2 C2ORF3,CYGF,DNABF,GCF,GCFC2,GC_F,GUC2DL,GUCY2F,RETGC2,RETGC_2,ROSGC2,ROS_GC2,TCF9
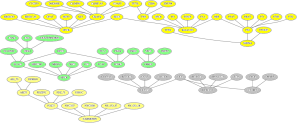
Ele encontrou 4 componentes conexas, cada uma em uma linha. Isso indica que todos os genes na mesma linha são sinônimos. A versão em grafo seria:
E como normalizar?
Para normalizar é preciso eleger um nome dentro de cada CC e substituir todos os outros nomes por ele. Isso vai depender do problema e de como ele é apresentado. Basicamente, rode um “sed” ou equivalente para trocar todos os nomes de um conjunto pelo nome eleito daquele conjunto. Não mostrarei tal implementação aqui, se precisar de ajuda é só postar nos comentários.
Conclusão
Um problema comum é encontrar os sinônimos para uma mesma entidade tal que os nomes estão espalhados por todo um arquivo de entrada. Vimos que para agrupar todos os sinônimos é necessário considerar o arquivo de entrada como um grafo, em que cada nome é um vértice e uma aresta indica que os vértices são sinônimos, e a solução é encontrar todas as componentes conexas desse grafo.
Referências
[1] “Find Connected Components in a Graph” by breakingcode (http://archive.is/VAcdP) (Acessado em: Outubro/2016)
http://breakingcode.wordpress.com/2013/04/08/finding-connected-components-in-a-graph
[2] Connected component (graph theory) by wikipedia (http://archive.is/OQN1h) (Acessado em: Outubro/2016)
https://en.wikipedia.org/wiki/Connected_component_%28graph_theory%29